On peut démontrer que les
scies à 
format ont des dispersions non négligeables, c’est à
dire que les cotes fabriquées varient autour d’une
moyenne avec
un écart plus ou moins important suivant leur précision. Cette
méthode s'appelle le SPS, Statistic Process Control.
Le travail proposé consiste
à caractériser ce phénomène et d'en préciser les causes.
A
cet effet je vous propose un prélèvement de 50 pièces
consécutives sur un lot de pièces à la sortie de la scie à
format qui sont classées dans l'ordre de 1 à 50 au fur et à mesure
de leur usinage.
L’objectif est de vérifier si la dispersion des valeurs obtenues
répond à une loi normale à l’aide d’un papier Gausso-arithmétique
et de vérifier la capabilité de la machine à réaliser la cote
dans l'intervalle donné.
-
Matériels à disposition :
Votre
cerveau !
a
-
Partie 1 - préparation et essais
Comme vous
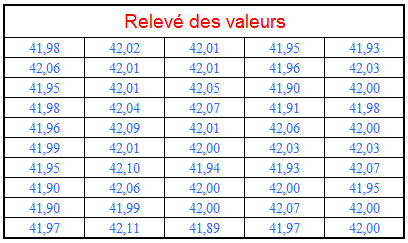
ne pouvez pas le réaliser, je vous donne un tableau de relevés de cotes de longueur de chaque pièce dans l’ordre de
réalisation sur la scie à format. On lit l'ordre de réalisation
de haut en bas de gauche à droite.
b
Partie 2 - Contrôle et exploitation.
A partir
du tableau du relevé des valeurs ci-dessus on souhaite
caractériser la capabilité de la machine, c'est à dire la
capacité de la machine à réaliser les cotes dans l'intervalle de
tolérance donné.
-
L'explication de la méthodologie à suivre pour obtenir ce
résultat est proposée ci-dessous :
- Tracer
le film de production relatif à ce prélèvement (graphique
chronologique représentatif de la distribution) sur papier
millimétré ou quadrillé à petits carreaux (5mm) avec une grande
échelle 0.1 mm = 10 cm.
-
Construire l’histogramme représentatif de la répartition de ces
échantillons après
en avoir calculé les différents paramètres : valeurs mini maxi,
l'étendue w, le nombre de classes n, la largeur des classes, l'effectif de
chaque classe, la fréquence relative par classe et la fréquence cumulée
des classes.
-
Vérifier alors si la population obéit à une loi normale, (c'est
à dire si ma courbe a plus ou moins une forme de cloche) en utilisant
le papier Gausso-arithmétique du test de la droite de Henry –
Annexe 2. Puis extraire de la droite, la moyenne et l’écart
type.
Je
rappelle qu'un écart type sur une courbe de Gauss est la valeur
où se situe le point d'inflexion, c'est a dire le point où la
courbe change d'orientation.
–
Calculez ensuite, la moyenne et l’écart type à partir de
l’échantillon avec une calculatrice.
- Comparez
les deux moyennes et les deux écarts types, puis conclure quant
à la pertinence de la méthode graphique.
-
Rechercher les causes qui pourraient engendrer les variations
des cotes.
- En
utilisant l’écart type de votre choix, calculer la capabilité de
la scie à format pour une cote de .
On donne
la formule de la capabilité machine Cm :
Cm =
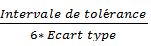
Remarque : Vous trouverez
en bas de pages des illustrations des éléments décrits
ci-dessus.
1 - Tracer
le film de la production dans l'ordre de réalisation.
2 -
Définir les valeurs limites mini maxi relevées dans le tableau.
3 -
Calculer l'étendue W = valeur maxi - valeur mini.
4 -
Définir le nombre de pièces n.
5-
Déterminer le nombre de classes N =
,
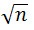6 -
Déterminer la largeur de classe Lc = W/ N. (Formule
corrigée)
7 – Pour
chaque classes, définir limite inférieure, limite supérieure et
le centre de classe xi.
8 -
Dénombrer pour chaque classes, les effectifs (le nombre de pièce
situées dans la classe) ni
puis vous calculerez l'effectif cumulé de chaque classe.
9 - A
partir de la question précédente, calculer les fréquences relatives par classe fi, et les
fréquences cumulées en pourcentage.
10 -
Calculer la moyenne X de l'échantillon de 50 pièces avec
votre calculatrice.
11 -
Calculer l'écart type s de l'échantillon de 50 pièces avec votre
calculatrice,
12 –
Vérifier par la droite de Henry la normalité de la distribution.
Vous pouvez utiliser le document annexé au support.
13 -
Tracer la droite de Henry à l'aide de la méthode ci-dessous.
14 -
Extraire de votre tracé de la droite de Henry la moyenne de
l'échantillon X' et l'écart type s' puis comparez X et X', s et
s'.
15 - La
méthode graphique vous semble-t-elle fiable ? Justifiez votre
réponse.
- Méthodologie
de tracé de la droite de Henry :
- Sur
l'axe des abscisses définir l'échelle pour porter l'étendue et les valeurs
des classes en utilisant la plus grande longueur possible sur l’axe
afin de minorer les erreurs.
- Sur
l'axe des ordonnées prendre les valeurs des fréquences cumulées
correspondant aux différentes classes et les reporter
progressivement sur les centres des classes.
- Tracer
la droite de Henry qui passe au plus juste de tous les points
avec une règle. le tracé n'est pas une succession de segments
mais un seul trait. D'où l'importance à attacher au
positionnement de la règle.
- La moyenne
se calcule en prenant le point d'intersection de la droite de
Henry et le trait matérialisant les 50%, puis en projetant ce
point verticalement sur l'axe des abscisses. Il ne vous reste
plus qu'à lire la valeur au point d'intersection. .
-
L'écart
type se calcule en projetant les deux points d'intersections
avec les deux lignes en pointillés matérialisant le moyenne plus
ou moins un écart type. La projection orthogonale de ces deux
poits sur l'axe des abscisses vous donnera la valeur de deux
écarts types. En divisant par deux votre résultats vous aurez la
valeur d'un écart type.
Remarque : le papier Gausso-arithmétique est un papier avec
en abscisse une échelle arithmétique et en ordonnée une échelle
gaussienne en pourcentage, l'intérêt du papier Gausso-arithmétique
est qu'il permet de transformer une courbe de Gauss en une
droite qui est plus facilement exploitable. Cette droite
s’appelle la droite de Henry.
