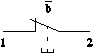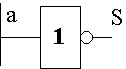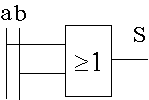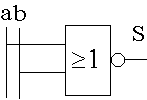|
Logique binaire
L'algèbre de Boole est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques. Le nom provient de George Boole. George Boole est le fondateur de la logique moderne. L'algèbre de Boole est une algèbre permettant de traduire des signaux (tout ou rien) en expressions mathématiques en remplaçant chaque signal élémentaire par des variables logiques et leur traitement par des fonctions logiques. L'algèbre de Boole permet de résoudre des équations logiques afin de réaliser des fonctions sur des signaux numériques. Ces fonctions seront appelées fonctions combinatoires L'algèbre de Boole des fonctions logiques permet de modéliser des raisonnements logiques, en exprimant un « état » en fonction de conditions. un mathématicien britannique qui, durant le milieu du XIXe siècle, restructura complètement la logique en un système formel. Plus spécifiquement, l'algèbre booléenne permet d'utiliser des techniques algébriques pour traiter les expressions à deux valeurs de la logique des propositions. Aujourd'hui, l'algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques. Un circuit électrique, électronique ou pneumatique, peut avoir 2 états logiques. Ces états peuvent prendre les valeurs 1 ou 0. Ces états sont fonctions de l'état des composants en série dans le circuit. Les actionneurs tels que : moteurs, vérins sont à l'état 0 lorsqu'ils ne sont pas alimentés. Le circuit est alors ouvert. Pour un circuit pneumatique ceci correspond à une absence de pression. Pour un circuit électrique cela correspond à une absence de différence de potentiel entre les bornes du circuit. Pour un contact ou un distributeur, c'est l’absence d'action physique intervenant sur un contact qui représente l'état 0. Les actionneurs sont à l'état 1 lorsqu'ils sont alimentés. Pour un circuit pneumatique ou hydraulique ceci correspond à une pression d’air ou d’huile dans le circuit. Pour un circuit électrique cela correspond à une différence de potentiel entre les bornes du circuit. Pour un contact ou un distributeur ils sont actionnés, c’est à dire qu'une action physique est prise en compte.
Un circuit électrique est dit passant, ou fermé, lorsqu'un courant électrique circule dans ce circuit. Cela implique qu'il y ait continuité de ce circuit, c’est à dire que le contact établisse le circuit. Un circuit électrique est non passant, ou ouvert, si le courant ne peut pas circuler dans ce circuit. Un circuit électrique comprend au minimum, une source d'énergie, un récepteur et un contact.
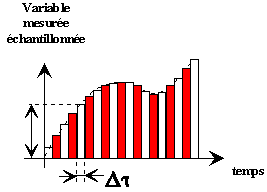
En automatique trois types de signaux sont utilisés principalement. Les signaux analogiques, numériques et tout ou rien.
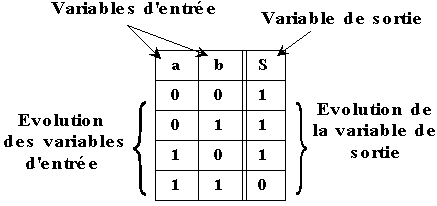
Une table de vérité est la représentation de l’évolution du comportement d’un système automatisé en fonction des variations de ses entrées. Chacune des variables est représentée sous une écriture binaire. Une table de vérité s'utilise principalement en logique combinatoire. Elle est représentée sous la forme suivante :
Un logigramme est un schéma représentant une succession de symboles logiques permettant d’obtenir par combinaison de variables d’entrées la sortie recherchée. Attention, les fonctions logiques sont des opérateurs logiques et non des opérateurs mathématiques. Le résultat obtenu sera un résultat logique et non un résultat mathématique. Exemple d’écriture :
Le code binaire pur est une représentation numérique en base deux. Cette représentation permet de représenter des nombres sous forme de 1 et de 0, ou de décrire l’évolution des variables vraies ou non vraies d’un système automatisé, c’est cette possibilité que nous allons utiliser. Le nombre de combinaisons possibles des variables se calcule de la façon suivante :
Lorsque l’on regarde ligne par ligne l’évolution du code binaire pur, on remarque que pour passer d’une ligne à l’autre, plusieurs variables peuvent être amenées à changer de valeur simultanément. Ceci est très gênant lorsque l’on cherche à analyser le comportement d’un système en fonction de ses entrées. Un autre code binaire a été mis au point, c’est le code binaire réfléchi ou code GRAY du nom de son inventeur. Ce code permet de passer d’une ligne à l’autre de la description d’un système avec l’évolution d’une seule variable à la fois. Ce code permettra de définir l’évolution d’un système automatisé. En aucun cas il ne pourra servir de base de comptage comme le binaire pur. On utilisera ce codage ultérieurement dans ce cours pour la définition des tableaux de Karnaugh. Exemple :
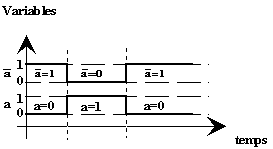
Nous avons vu précédemment qu’une variable "e" avait deux
états, l’état 0 et l’état 1. Si on admet qu’il peut exister une
variable " Exemple :
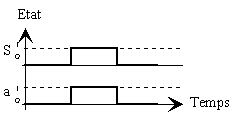
Les fonctions logiques sont des opérateurs logiques. C’est à dire qu’en fonction d’une ou plusieurs variables données, ils vont répondre par une sortie particulière. Le symbole "Ξ" se lit "équivalent" pour bien distinguer le résultat logique d’un résultat mathématique. - Equation : S Ξ a - S reproduit la variable d’entrée a.
- Equation : S
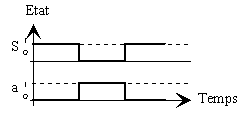
Ξ - S reproduit l’inverse de la variable d’entrée a.
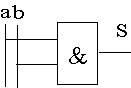
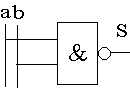
- Equation : S Ξ a . b - S reproduit le produit des variables d’entrée a et b.
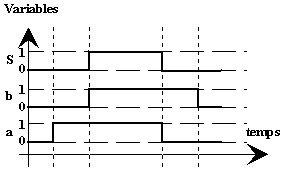
- Equation : S Ξ a + b - S reproduit la somme logique des variables d’entrée a et b.
- Equation
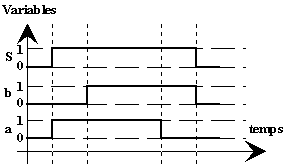
: S Ξ - S reproduit l’inverse de la somme logique des variables d’entrée a et b.. La fonction NOR (ou NI) est une fonction universelle, c’est à dire que les fonctions OUI, NON, OU, ET peuvent être réalisées avec uniquement des opérateurs NOR.
- Equation : S Ξ - S reproduit l’inverse du produit logique des variables d’entrée a et b. La fonction NAND est aussi une fonction universelle.
- Equation : S
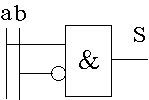
Ξ a . - S reproduit le produit logique d’une variable d’entrée a et du complément d’une variable d’entrée b.
Le complément d’un produit logique de variables est égal à la somme logique des compléments de variables.
Le complément d’une somme logique de variables est égal au produit logique des compléments de variables.
C’est une logique de combinaison de variable, c’est à dire que pour une combinaison d’entrées donnée, il ne correspond qu’une et une seule sortie. Les différentes fonctions logiques utilisées jusqu’à maintenant fonctionnent en logique combinatoire. Schéma :
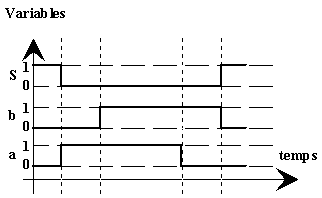
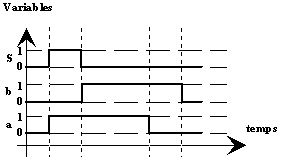
Exemple : Lorsque le conducteur d’un véhicule fait un appel de phares, les phares resteront allumés tant que le conducteur appuiera sur la commande de phares. Nous sommes donc en présence d’un système combinatoire. C’est une logique qui fait intervenir en plus de la combinaison de variables d’entrées donnée, l’état dans lequel se trouve le S.A à un instant donné. Une sortie ne sera donc plus accessible directement par une combinaison d’entrées, il faudra aussi que le système soit dans un état déterminé pour pouvoir atteindre la sortie que l’on souhaite. Le grafcet que nous étudierons dans un prochain chapitre fonctionne aussi en logique séquentielle. Schéma :
La fonction mémoire est réalisée par un opérateur logique qui peut stocker une information jusqu’à ce que cette information soit effacée par une autre information. L’opération de stockage d’information s’appelle "SET" (Mise à un) l’opération d’effacement s’appelle "RESET" (Mise à zéro). Ces opérateurs peuvent être électriques, électroniques, pneumatiques... Les bascules logiques sont les éléments les plus simples qui constituent les mémoires. Un tableau de Karnaugh est un tableau représentatif du comportement d’une variable. Ce tableau a pour but de simplifier l’écriture de l’équation de fonctionnement. Il est utilisé principalement en logique combinatoire. Dans ce tableau chaque case correspond à une combinaison d’entrées de la variable. Dans chaque case on reporte l’état de la variable [0,1]. Exemple :
La variable de sortie S est active dans deux cas. Les deux combinaisons de
sortie sont respectivement pour a et b, [0,0] ou [0,1]. L’utilisation du
tableau de Karnaugh permet de déterminer très rapidement l’équation de la
variable S. Il faut rechercher les variables qui n’influent pas le
comportement de la variable de sortie. Dans notre exemple les 1 sont dans une
colonne, le résultat va donc dépendre directement de la variable associée à
cette colonne, ici "a". La variable de ligne n’a pas d’influence
car quel que soit l’état de b (0 ou 1), la variable de sortie reste à 1. L’équation
de sortie sera donc S º Lorsqu’un système présente 4 variables d’entrée le principe est le même. Il faut remarquer la construction de ce tableau. Sur l’exemple suivant, on remarque :
Exemple : pour passer de la première colonne du tableau [a,b] º [0,0] à la dernière colonne [a,b] º[1,0] seule la variable "a" a évolué.
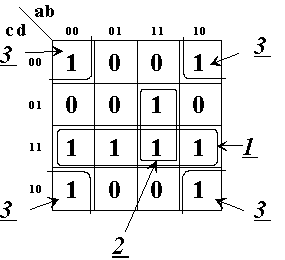
Ce tableau doit être complété par l’état de la sortie à analyser. Une fois terminé on procédera par regroupement des cases indiquant des états identiques par rapport aux axes de symétrie. Exemple :
Le groupement 3 se fait sur deux lignes et deux colonnes, ici ce cas est particulier puisque les cases ne sont pas contiguës, mais il est possible. L’équation va dépendre des variables "b, d" et non des variables a, c puisque ces variables changent d’état. L’équation de ce groupement est : "b.d". L’équation de fonctionnement de S devient :
On constate, pour un tableau de 16 cases, qu’un regroupement de 2 cases donne un élément d’équation à 3 variables, qu’un regroupement de 4 cases donne un élément d’équation à 2 variables. On peut en conclure qu’un regroupement d'une seule case donnera un élément d’équation à 4 variables qu’un regroupement de 8 cases donnera un élément d’équation à 1 variable, qu’un regroupement de 16 cases donnera une équation de fonctionnement toujours vraie. |